• 1. Node-level Features
• 2. Link-Level Features
• 3. Graph-Level Features
  • 1) Kernel method
  • 2) Graph Kernels
• 4. Random Walk 임베딩
  • 1) Random walk란?
  • 2) 임베딩 과정
  • 3) How should we randomly walk?
• 5. Embedding Entire Graphs
  • 1) Approach 1
  • 2) Approach 2
  • 3) Approach 3

1. Node-level Features

• Node degree: node가 가지고 있는 edge 수
• Node centrality: 그래프안에 node의 중요도
  • Eigenvector centrality: 주변 노드의 중요도를 합해서 계산함. 행렬 연산으로 표현 가능.
  • Betweenness centrality: node들간의 최단거리에 가장 많이 놓인 노드가 중요하다.
  • Closeness centrality: 다른 node들까지 경로의 합이 작을 수록 중요하다.
• Clustering coefficient: v의 이웃 노드들이 서로 연결될 수 있는 edge 개수 중 얼마나 실제로 연결되어 있는가를 측정함.
• Graphlets: pre-specified subgraph의 개수를 세서 측정 가능

2. Link-Level Features

• Distance-based feature
  • 두 노드 간 최단거리에 기반
• Local neighborhood overlap
  • 공통된 이웃 숫자
  • jaccard’s coefficient: 공통된 이웃 숫자를 각 노드가 가지고 있는 이웃수의 합으로 나누어 정규화
  • adamic-adar index: 이웃 노드의 degree까지 고려
• Global neighborhood overlap
  • katz index: node 쌍간의 walk의 수

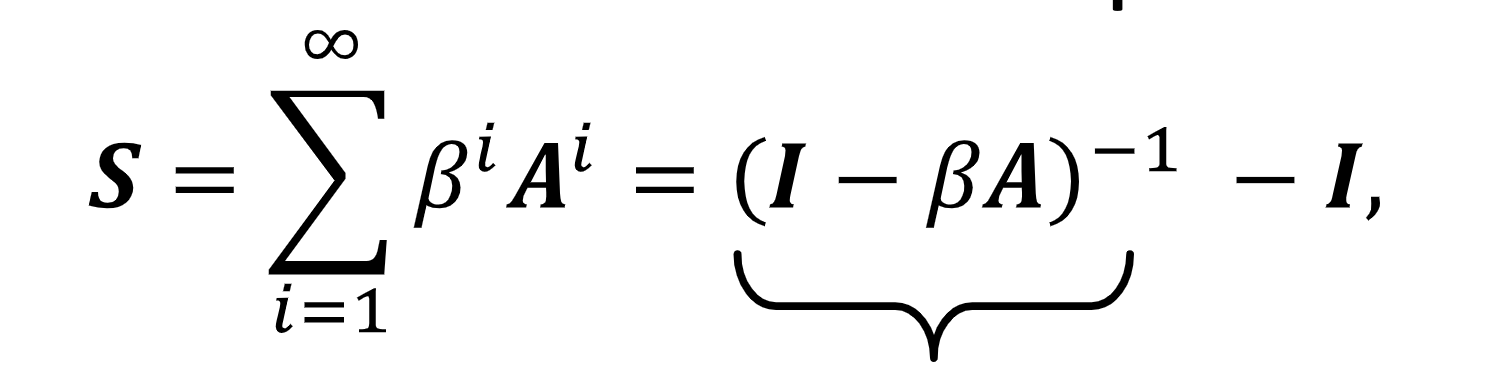
3. Graph-Level Features

1) Kernel method

• Kernel K(G, G’)은 두 데이터간의 유사도를 측정한다.
• Kernel matrix K는 항상 positive semidefinite해야 한다.
• K(G, G’)를 $\phi(G)^T\phi(G’)$ 형태로 표현할 수 있게 하는 $\phi$가 존재한다.

2) Graph Kernels

(1) Graphlet Kernel

• K(G, G’) = $f_G^T f_{G’}$
• f는 graphlet count이다.
• 비용 비효율적이다.

(2) Weisfeiler-Lehman Kernel

$c^{k+1}(v) = HASH({c^{k}(v),{c^{k}(u)_{u\in N(v)}} })$

• 위 식을 이용해 각 노드의 color를 계산하고 최종적으로 각 color의 count를 세어 embedding vector를 비교하는 방식을 사용한다.

4. Random Walk 임베딩

1) Random walk란?

Random Walk: graph에서 무작위로 starting point를 고르고, 이웃으로 이동한다.

장점: local과 neighborhood 모두 반영할 수 있다는 expressivity와 학습 중에 모든 node 쌍을 살펴볼 필요가 없다는 효율성이 있다.

2) 임베딩 과정

Objective:

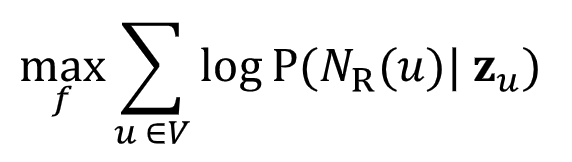
embedding이 neighborhood를 나타낼 수 있는 확률을 높일 수 있도록 학습시키겠다는 의미를 담고 있다. loss function으로 바꾸어보면 다음과 같다.

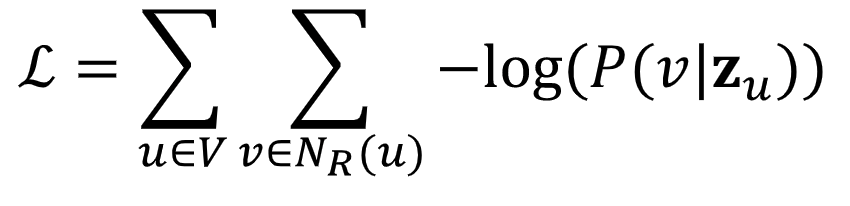
여기서 확률값은, node v가 node u와 most similar하기를 바라는 것이기에 다음과 같이 표현할 수 있다.

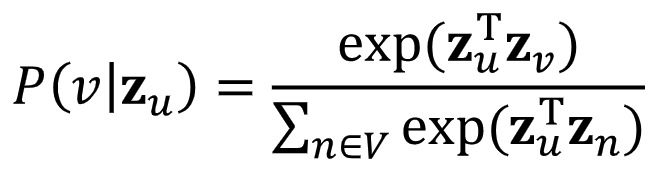
모든 노드에 대해 nested sum을 구하는 것은 많은 시간복잡도를 요구하는 일이다.

negative sampling을 통해 시간을 단축할 수 있다. (https://arxiv.org/pdf/1402.3722.pdf)

3) How should we randomly walk?

가장 단순한 idea: just run fixed-length

idea 고도화: bfs(local microscopic view)와 dfs(global macroscopic view)를 잘 조합해보자. 다음과 같이 두 개의 파라미터를 조정해서 조율한다.

Return parameter p: 이전 노드로 돌아가는 비율

In-out parameter q: Bfs와 Dfs의 비율

5. Embedding Entire Graphs

1) Approach 1

각 node의 embedding을 구한 다음, 모든 node의 embedding의 average를 취한다.

2) Approach 2

graph를 표현할 수 있는 virtual node를 추가한다.

3) Approach 3

Anonymous walk를 이용하는 방법:

• Generate independently a set of 𝑚 random walks.
• Represent the graph as a probability distribution over these walks.

얼마나 많은 random walk를 수행해야 할까?

• anonymous walk를 time state에 따라 나누어 사용하는 방법도 있지만, next walk를 예측할 수 있도록 embedding 을 학습시켜보자.