Planarity
1. Planar graphs
planar graph: graph G를 평면에 그렸을 때 꼭짓점이 아닌 곳에서는 어떤 점도 교차하지 않는 graph
plane graph: planar graph가 최대한 교차 없이 그려졌을 때 plane graph라고 함.
simple planar graph: graph가 simple하고 planar함.
Thm 12.1
$K_{3,3}$ (Bipartite graph) and $K_5$(complete graph)은 non-planar이다.
homeomorphic: 두 그래프가 같은 그래프에서 degree가 2인 vertex들을 추가해 얻을 수 있는 것일 때
Kuratowski’s thm
A graph is planar if and only if it contains no subgraph homeomorphic to $K_5$ or $K_{3,3}$.
contractible: 어떤 graph에서 edge들을 제거해 $*K_5$ or $K_{3,3}$*를 얻을 수 있을 때
Thm 12.3
A graph is planar if and only if it contains no subgraph contractible to $K_5$ or $K_{3,3}$.
pf) Kuratowski’s thm에서 유도 가능
crossing number: 특정 graph가 plane에 그려졌을 때 가장 적은 수의 crossing을 cr(G)라고 한다.
2. Euler’s Formula
faces: G가 planar graph일 때, G의 plane drawing은 plane을 face라 불리는 region들로 나눈다.
infinite face: bound가 없는 face
Thm 13.1
G가 완전 연결 planar graph가 plane위에 그려진 형태라고 하고, n, m, f가 vertex, edge, face의 개수라고 했을 때, n - m + f = 2 이다.
graph의 number of edges에 대한 induction으로 증명할 수 있음.
Corollary 13.2
Let G be a polyhedral graph. Then, with the above notation, n - m + f = 2.
Corollary 13.3
Let G be a plane graph with n vertices, m edges, f faces and k components. Then n - m + f = k + 1
Corollary 13.4
(i) G가 n(≥3) vertices와 m edges를 가진 단순 연결된 planar graph일 때, m≤ 3n-6이다. (ii) G에 삼각형이 없다면, m≤2n-4이다.
(i)는 3f≤2m 이라는 사실로부터 나온다. (모든 face는 적어도 3개의 edge로 둘려싸여 있다!)
Thm 13.6
모든 simple planar graph는 degree가 최대 5인 vertex를 포함하고 있다.
thickness (t(G)): the smallest number of planar graphs that can be superimposed to form G.
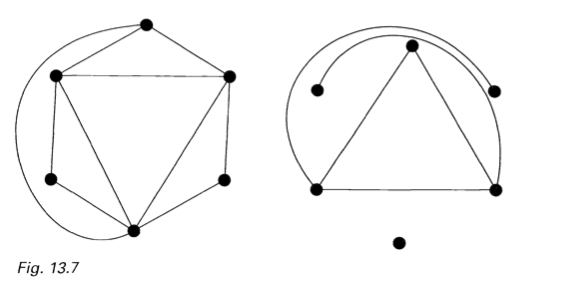
$K_6$의 thickness는 2이다.
Thm 13.7
G를 n(≥3) vertices와 m 개의 edge로 구성된 단순 graph라고 하자. 이때 t(G)는 다음과 같은 부등호를 만족한다.
${t(G)\ge \lceil m/(3n-6) \rceil}$ and ${t(G)\ge \lfloor (m+3n-7)/(3n-6) \rfloor}$
${\lceil a/b \rceil = \lfloor(a+b-1)/b\rfloor}$ 에서 유도할 수 있다.
3. Graphs on other surfaces
genus g: topologically homeomorphic to a sphere with g handles.
graph of genus g: genus g에 crossing없이 그려질 수 있지만, genus g-1에는 불가능한 graph를 graph of genus g라고 부른다. $K_5$와 $K_{3,3}$은 graph of genus 1이다.
Thm 14.1
graph의 genus는 crossing number를 초과하지 않는다.
crossing이 있는 곳에는 handle을 추가해 crossing을 없앨 수 있다.
Thm 14.2
G가 n vertices, m edges, f faces를 가진 genus g의 연결 graph라고 하자. n-m+f = 2-2g이다.
pf) sphere 형태에서 handle을 만들기 위해서 면을 2개 제거해야 한다. handle 하나 당 2개의 면이 제거되기에 기존의 오일러 공식에서 2g를 빼주면 된다.
Corollary 14.3
n(≥4) vertices와 m edges를 가지고 있는 단순 그래프 G의 genus(G)는 다음 부등식을 만족한다. g(G) ≥ $\lceil(m-3n)/6+1\rceil$
pf) 앞서 planar의 예시와 비슷하게 하나의 face는 적어도 3개의 edges로 둘러싸여져 있다는 사실을 이용하면 된다. 하나의 edge는 두개의 face에 영향을 주기에 3f≤2m 이다.
→ $g(K_n)\ge\lceil(n(n-1)/2-3n)/6+1\rceil$
→ $g(K_n)\ge\lfloor(n-3)(n-4)/12\rfloor$
Thm 14.4 (Ringel and Youngs)
$g(K_n)=\lceil(n-3)(n-4)/12\rceil$
4. Dual graphs
(geometric) dual of G; G*: (i) 각 G face안에 vertex를 하나씩 찍는다.
(ii) G의 각 edge를 교차시키는 edge를 하나씩 그린다. 단 이 edge는 두개 이상의 edge를 교차하지는 않는다. 교차된 edge를 이용해 (i)에서 만든 vertex들 사이에 edge를 만든다. 추가한 vertex와 edge로 이루어진 graph가 G의 geometric dual이다.
G가 H에 isomorphic하다고 해서, G이 H에 isomorphic한 것은 아니다.
Lemma 15.1
G를 n개의 vertex, m개의 edge, f개의 face를 가진 plane이라 하고, geometric dual한 그래프 G이 n vertices, m* edges, f* faces를 가졌다고 했을 때, n* = f, m* = m, f* = n임을 알 수 있다.
pf) dual graph를 그리는 과정을 생각해보자!
Thm 15.2
G가 plane connected graph일 때, G**은 G에 isomorphic하다.
pf) G*에서 G를 다시 복구하는게 G**을 그리는 것과 똑같기에 당연하다.
Thm 15.3
G가 planar graph이고 G가 G의 dual이라고 하자. G에서 edges들이 cycle을 이루는 필요충분조건은 해당 edges에 mapping되는 G의 edge들이 G*에서 cutset을 구성할 때이다.
Corollary 15.4
A set of edges of G forms a cutset in G if and only if the corresponding set of edges of G forms a cycle in G.
15.3에서 G와 G*을 바꿔 생각하면 증명할 수 있다.
abstract dual: G의 edge들과 G의 edge들이 1-1관계를 가지는데, 이 때 어떤 edge가 G에서 cycle을 만들면 G에서 그에 대응되는 edge는 G*의 cutset을 구성해야 한다.
Thm 15.5
G이 G의 abstract dual이면, G는 G의 abstract dual이다.
cycle의 cutset에 있는 edge의 수는 even이라는 사실과 G의 이 edge-disjoint union이라면 G의 cycle에 매핑되는 G의 cutset의 수도 적어도 두 개의 cutset이 있어야 한다는 사실을 이용해 증명할 수 있다.
Thm 15.6
graph가 planar가 되기 위한 필요충분 조건은 graph가 abstract dual을 가질 때이다.
pf)
(i) G has an abstract dual, then so does any subgraph of G
(ii) G has an abstract dual, and G is homeomorphic to G, then G’ also has an abstract dual.
(iii) neither $K_5$ **nor $K_{3,3}$ has an abstract dual
(iv) G is a non-planar graph with an abstract dual G*
5. Infinite graphs
infinite graph: an infinite set V(G) vertices와 infinite family E(G) edges
countable graph: V(G)와 E(G)가 countably infinite하면 G도 countable graph이다.
locally finite: infinite graph의 vertex가 finite degree를 가졌으면 locally finite하다.
locally countable: infinite graph의 vertex가 countable degree를 가졌으면 locally countable하다.
Thm 16.1
모든 연결된 locally countable infinite graph는 countable graph이다.
Corollary 16.2
모든 연결된 locally finite infinite graph는 countable graph이다.
Konig’s lemma
G가 연결된 locally fininte infinite graph일 때, G의 아무 정점 v에 대해, initial vertex v로 시작하는 one-way infinite path가 존재한다.
Thm 16.4
G가 countable graph일 때, 모든 finite subgraph가 planar이면, G도 planar이다.
Thm 16.5
G가 연결된 countable Eulerian graph라고 하자. (i) G는 odd degree를 가진 vertex를 가지지 않는다. (ii) G의 각 subgraph H에 대해, G에서 H의 edges를 제거해 얻어지는 H graph는 최대 두 개의 infinite connected components를 가진다. (iii) 추가로, subgraph H가 even degree를 가진다면, H는 정확히 하나의 infinite connected component를 가진다.
Thm 16.6
만약 G가 연결된 countable graph라고 할 때, G가 Eulerian이기 위한 필요 충분 조건은 Thm 16.5의 조건들을 모두 만족할 때이다.
