• Relational Graph Convolutional Network (Relational GCN)
  • (1) Scalability
  • (2) 학습 방법
• Knowledge Graphs (KG)
• Knowledge Graph Completion (KG Completion)
  • (1) TransE
  • (2) Relation Patterns
  • (3) TransR
  • (4) DistMult
  • (5) ComplEx

Heterogenous Graph란?

• Nodes with different types
• Edges with different types
• Every nodes & every edges are labelled by it’s type.

Relational Graph Convolutional Network (Relational GCN)

notion: GCN for Heterogenous graph

${h_v^{l+1} = \sigma(\Sigma_{r \in R}\Sigma_{u \in N_v^r}(1/c_{v,r})W_r^{l}h_u^{l}+W_0^{l}h_v^l)}$

relation마다 다른 type의 가중치 matrix를 사용하겠다는 아이디어다.

(1) Scalability

Relation 개수의 증가는 학습 파라미터 수의 급격한 증가로 이어진다. -> Overfitting 발생

• Use Block diagonal matrices
  • weight matrix를 Sparse하게만 사용한다.
  • 근처에 있는 neuronss/dimensions만 W를 통해 interaction할 수 있다.
• Basis/Dictionary learning
  • 다른 relation에 공유 가중치 사용
  • relation에 대한 matrix를 basis transformations의 linear combination으로 생각

(2) 학습 방법

• Heterogenous한 graph이기 때문에 각 type별 분포가 train/valid/test set모두에서 똑같도록 조정이 필요함
• train set의 graph에서 연결되지 않은 node는 연결되지 않았음을 학습시키는 것도 필요함

Knowledge Graphs (KG)

Notion: Bibliographic Networks와 같이 relation에 대한 특정 fact를 캡쳐하는 네트워크로 Heterogenous graph의 일종임.

• Application:

  • Serving Information
  • Question answering and conversation agents

• Datasets

  • Publicly available KGs: FreeBase, Wikidata etc
  • 공통점: 거대하고 불완전한 데이터셋임

Knowledge Graph Completion (KG Completion)

Notion: head(h)와 relation(r)이 주어졌을 때, 연결되지 않은 tail(t)들을 찾는다.

💡 Key Idea: (h,r)의 embedding이 t의 embedding과 비슷해야 한다.

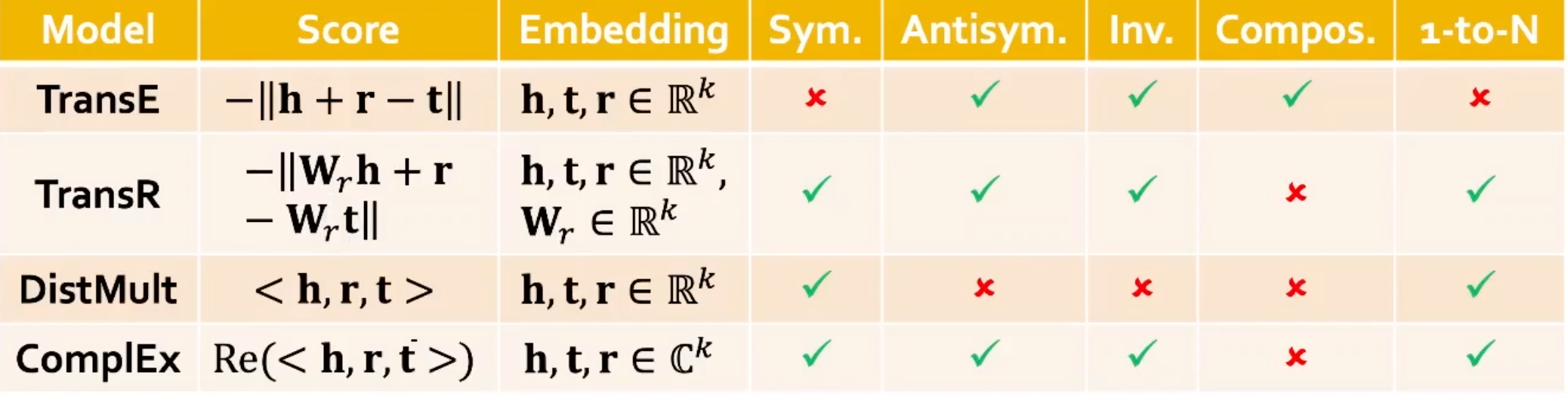
(1) TransE

(h,r,t) triple에 대해서, tail이 relation을 통해 head와 연결되어 있으면 ${h + r\approx t}$이고, 거짓이라면 ${h+r \neq t}$이 되게 벡터들을 학습시킨다.

Scoring function: ${f_r(h,t)=-||h+r-t||}$

학습 방법은 다음과 같다.

교수님이 학생을 바라보는 relation과 학생이 교수님을 바라보는 relation이 다르듯이, Heterogenous KG안에 있는 relation은 여러가지 성질을 가지고 있다. TransE는 다양한 relation을 표현할 수 있을까?

(2) Relation Patterns

• Symmetric(Antisymmetric Relations)

• Inverse Relations

• Composition (Transitive) Relations

• 1-to-N relations

이러한 relation들이 있는데, TransE는 symmetric한 relation과 1-to-N relation은 표현할 수 없다.

(3) TransR

Model entity를 표현하는 vector와 relation을 표현하는 vector의 차원이 달라지고, model entity vector를 relation을 표현하는 vector에 projection하는 matrix를 학습시킨다.

${h_\perp=M_rh, t_\perp=M_rt}$

Scoring function: ${f_r(h,t)=-||h_\perp+r-t_\perp||}$

하지만, TransR은 composition relation을 학습할 수 없다.

(4) DistMult

Entity들과 Relation들이 같은 차원에 있는 vector를 이용하며, scoring function으로는 다음 함수를 이용한다.

${f_r(h,t)=<h,r,t>=\Sigma_ih_ir_it_i}$

직관적으로 생각했을 때, ${hr}$과 t의 cosine similarity 값과 같기 때문에 타당하다.

하지만, inverse relation을 modelling할 수 없다. 또한, union of the hyperplane은 single hyperplane으로 묘사될 수 없기에, composition relation도 modelling할 수 없다.

(5) ComplEx

Entity들과 relation들이 ${C^k}$에 있는 vector를 이용한다.

Scoring function: ${f_r(h,t)=Re(\Sigma_ih_ir_i\overline{t}_i)}$